Homography, Image Mosaics & Autostitching
Introduction
This project demonstrates how simple operations like shifting and averaging can achieve complex effects. The work is done on the Stanford Light Field Archive, that has some sample datasets comprising of multiple images taken over a regularly spaced grid
Homography
Given a pixel $p$ and its transformed pixel $p'$, we can set a linear system to recover the Homography $H$.
$
\begin{align*}
p' &= H p \\
\begin{bmatrix}
wx \\
wy \\
w
\end{bmatrix}
&=
\begin{bmatrix}
a & b & c \\
d & e & f \\
g & h & 1 \\
\end{bmatrix}
\cdot
\begin{bmatrix}
x \\
y \\
1
\end{bmatrix}
\end{align*}
$.
(The bottom right of $H$ is the scaling factor which is fixed at 1.)
(The bottom right of $H$ is the scaling factor which is fixed at 1.)
We can reformulate the linear system to solve for $a, b, c, ..., h$. Since the degree of freedom is 8, it is obvious that 4 sets of corresponding pixels $(p, p')$ will yield 8 equations, enough to solve using least squares.
Image Rectification
One of the most obvious application of homography is image rectification, essentially warping an image to "reangle" certain information. Here I ask user for at least 4 corresponding points, then solve the least squares problem to recover the homography. Here are some examples:
 |
 |
|---|---|
| Original Image | Rectified Image |
 |
 |
|---|---|
| Original Image | Rectified Image |
Creating Image Mosaics
We can now try to stitch images together to create mosaics. For each mosaic, I keep on image unwarped and try to warp the other image using some hand-picked feature points. Here are the results:
 |
 |
 |
|---|---|---|
| Original Left Image | Original Right Image | Mosaic |
 |
 |
 |
|---|---|---|
| Original Left Image | Original Right Image | Mosaic |
Autostitching (Automatic Point Selection)
Autostitching can be achieved by performing the following steps:
Feature Extraction: Detecting corner features in an image, and then extracting a Feature Descriptor for each feature point.
Feature Matching: Matching the feature descriptors between two images.
Compute Homography: Use a robust method (RANSAC) to compute a homography.
Feature Matching: Matching the feature descriptors between two images.
Compute Homography: Use a robust method (RANSAC) to compute a homography.
Feature Extraction
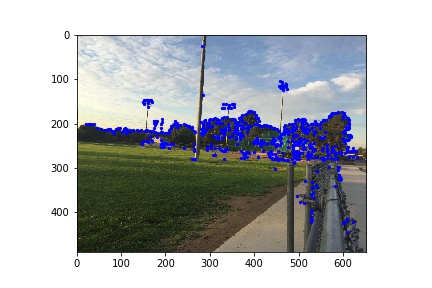
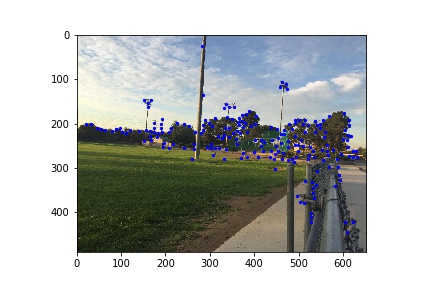
Here I used corner as featuers as they are rotation-invariant. First I used Harris Corner Detector to find all the corners in the two images.
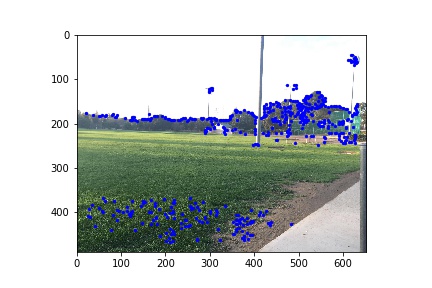 |
 |
|---|---|
| Left Image Corners | Right Image Corners |
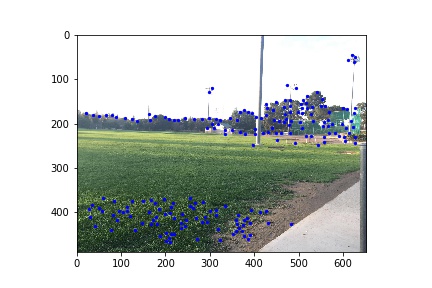
Since we are having too many corners, I used Adaptive Non-maximal Suppression to compute an optimal radius $r(p)$ for each corner p. Then I sorted the corners using the computed radius in descending order, and picked the first 200 corners.
 |
 |
|---|---|
| Left Image Selected Corners | Right Image Selected Corners |
Then we created 40-by-40 patches of pixels around the selected corners, and then downsampled them to 8-by-8 patches for robustness to rotation and scale. These patches will be used as features to match.
Feature Matching
To perform matching, we find pairs of features that look similar and are thus likely to be good matches.
RANSAC
hen, we run RANSAC with 1000 iterations and 4 random choices. In each iteration, we sample 4 pair of matched correspondences to calculate the projective transformation. Then we transform image 1 accordingly. In the end, we pick the set of points with most inliers, and use its homography and blend with picture 2 to get the mosaic. Here we also compare the results obtained from manual selections and auto selections
 |
|---|
| Park |
 |
|---|
| Trees |
 |
|---|
| Parking Lot |
Note: This is a class project for CS 194-26 Image Manipulation and Computational Photography taught by Professor Alexei Efros at UC Berkeley. Full description is available here.